7.2.1 - Les infrastructures de gestion de clés (IGC) :

7.2.1 - Les infrastructures de gestion de clés (IGC) :

Les techniques utilisées en cryptographie ont évoluées, passant de procédés gardés secrets à des algorithmes mathématiques connus utilisant des paramètres secrets que l'on a nommés « clés ».

Actuellement, la cryptographie classique (dite symétrique ou à clé secrète) repose sur ce principe.

Pour chiffrer un message, on utilise un algorithme répertorié ou correspondant à un standard s'appuyant sur un paramètre secret, la clé, qui est un nombre connu des différents interlocuteurs. Il est relativement facile de construire de tels algorithmes et seuls les besoins d'interopérabilité des systèmes de cryptographie limitent leur nombre.
Il existe deux systèmes de chiffrement :

le chiffrement symétrique,
le chiffrement asymétrique.

7.2.1.A - Le chiffrement symétrique :

7.2.1.A.1 - Principe :

Ils reposent sur le partage entre deux interlocuteurs en communication, d'une même clé secrète S qui sert à paramétrer un algorithme à la fois pour le chiffrement d'un message et pour son déchiffrement. La clé S doit faire l'objet d'un échange physique préalablement à toute communication.
Pour le stockage de messages chiffrés, le principe reste le même avec un seul interlocuteur.
Cette clé prend en général la forme d'un ensemble de bits de taille limitée.
En général, la clé secrète commune S n'est pas utilisée directement pour chiffrer les messages, mais pour chiffrer une autre clé K qui est un nombre tiré au hasard par l'émetteur à chaque session et qui sert comme clé secrète pour chiffrer les messages. Cette clé K chiffrée est envoyée en début de session ou de message ou, dans le cas de stockage, conservée avec le message.

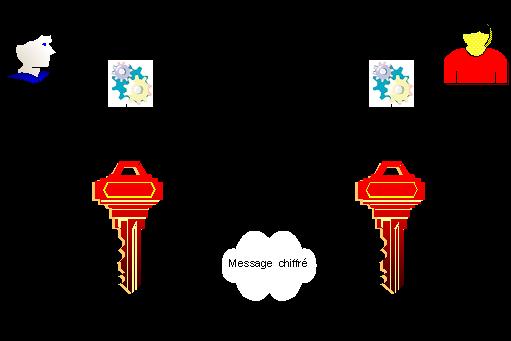
Exemple : Alice et Bob souhaitent communiquer de façon sécurisée. Ils ont besoin de se mettre d’accord sur l’algorithme de calcul utilisé pour chiffrer et déchiffrer les données. Ils ont alors besoin d’une clé commune : la clé secrète. Ils utilisent la même clé pour chiffrer et déchiffrer.

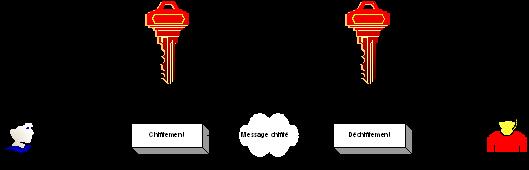
Figure 31 : Chiffrement symétrique

7.2.1.A.2 - Les différents algorithmes de chiffrement symétrique :

7.2.1.A.2.a - Le chiffre de César :

Le code de César est la méthode de cryptographie la plus ancienne communément admise par l'histoire. Il consiste en une substitution mono alphabétique, où la substitution est définie par un décalage de lettres. Par exemple, si on remplace A par D, on remplace B par E, C par F, D par G, etc...

Il n'y a que 26 façons différentes de chiffrer un message avec le code de César. Cela en fait donc un code très peu sûr, puisqu'il est très facile de tester de façon exhaustive toutes les possibilités. Pourtant, en raison de sa grande simplicité, le code de César fut encore employé par les officiers sudistes pendant la guerre de Sécession, et même par l'armée russe en 1915.

7.2.1.A.2.b - Le chiffre de Vigenère :

Blaise de Vigenère, né en 1523, fut l'initiateur d'une nouvelle façon de chiffrer les messages qui domina 3 siècles durant.
Blaise de Vigenère était diplomate au service des ducs de Nevers et des rois de France. C'est en 1586 qu'il publie son « Traité des chiffres ou Secrètes manières d'écrire » qui explique son nouveau chiffre.

L'idée de Vigenère était d'utiliser un chiffre de César, mais où le décalage utilisé change de lettres en lettres. Pour cela, on utilise une table composée de 26 alphabets, écrits dans l'ordre, mais décalés de ligne en ligne d'un caractère. On écrit encore en haut un alphabet complet, pour la clé, et à gauche, verticalement, un dernier alphabet, pour le texte à coder soit :

Figure 32 : Le chiffre de Vigenère

Pour coder un message, on choisit une clé qui sera un mot de longueur arbitraire. On écrit ensuite cette clé sous le message à coder, en la répétant aussi souvent que nécessaire pour que sous chaque lettre du message à coder, on trouve une lettre de la clé. Pour coder, on regarde dans le tableau l'intersection de la ligne de la lettre à coder avec la colonne de la lettre de la clé.

7.2.1.A.2.c - L’algorithme de Vernam :

Il existe un algorithme de chiffrement parfaitement sûr (il est d'ailleurs unique, comme l'a prouvé Shannon en 1949). Cet algorithme est tellement sûr qu’il est utilisé pour les communications au plus haut niveau : le téléphone rouge entre Moscou et Washington est codé grâce à lui. Cet algorithme a été mis au point par Gilbert Vernam en 1917, et est simplement un chiffre de Vigenère, mais où la clé est de la taille du message à envoyer, et où les lettres de cette clé sont choisies totalement aléatoirement. Si la clé ne sert qu'une fois (chiffre à usage unique), ce système est absolument sûr : il n'y a aucune corrélation entre le message de départ et sa version codée.

Les inconvénients de ce mode de chiffrement sont la génération et le transport des clés. Cette clé doit être parfaitement aléatoire, et sa longueur est énorme.... tout cela pour une seule utilisation!

Les cryptoanalystes ont donc été conduit à approcher ce mode de fonctionnement. A partir de clés de tailles rédigées (par exemple, codées sur 128 bits, ce qui est très peu par rapport à la longueur du message, typiquement, plusieurs milliards de bits). A partir de cette clé et du texte à coder qu'on découpe en blocs, on effectue des transformations toujours réversibles, mais suffisamment compliquées pour que le texte obtenu donne l'impression d'être aléatoire.

7.2.1.A.2.d - L’algorithme DES :

Les États-Unis, dans les années 1970, ont tenté d'imposer un algorithme, unique, baptisé DES (Data Encryption Standard), en insistant sur les problèmes d'interopérabilité et aussi de sécurité et d'économie. Pour cela, le département du Commerce a fait réaliser par la Société IBM un algorithme qui devait être publié, de manière à permettre son évaluation par tous, et qui devait être libre de tous droits d'usage. Plus de vingt ans après, la seule faiblesse révélée de cet algorithme est la longueur de la clé (56 bits), jugée trop courte pour les moyens de calcul actuels.
Même si le DES n'a jamais obtenu le statut de norme internationale, essentiellement pour des raisons politiques car certains États s'opposaient alors à la prolifération de dispositifs cryptographiques, il a été pendant des années l'algorithme employé de façon systématique dans le domaine commercial et reste aujourd'hui le plus employé. Il a quelques concurrents, essentiellement dans le domaine des produits logiciels, comme le RC4 ou IDEA, qui sont mieux adaptés à des implantations logicielles. Les applications gouvernementales utilisent pour des raisons de sécurité des algorithmes non publiés ; il en va de même dans le domaine des télécommunications où les opérateurs ont en général préféré définir leurs propres normes^[2].

La clé du DES est une chaîne de 64 bits (succession de 0 et de 1), mais en fait seuls 56 bits servent réellement à définir la clé. Les bits 8, 16, 24, 32, 40, 48, 56 et 64 sont des bits de parité (c'est-à-dire bits de détection d'erreur). Le 8ème bit est calculé de sorte que sur les 8 premiers bits, il y ait un nombre impair de 1. Par exemple, si les 7 premiers bits sont 1010001, le 8ème bit est 0. Ceci permet d'éviter les erreurs de transmission.

Il y a donc pour le DES 2⁵⁶clés possibles, soit environ 72 millions de milliards possibilités.

Les grandes lignes de l'algorithme sont :

Phase 1 : Préparation - Diversification de la clé :

Le texte est découpé en blocs de 64 bits.
On diversifie aussi la clé K, c'est-à-dire qu'on fabrique à partir de K 16 sous-clés K1,...,K16 à 48 bits. Les K_i sont composés de 48 bits de K, pris dans un certain ordre.

Phase 2 : Permutation initiale :

Pour chaque bloc de 64 bits x du texte, on calcule une permutation finie y=P(x).
y est représenté sous la forme y=G₀D₀, G₀ étant les 32 bits à gauche de y, D₀ les 32 bits à droite.

Phase 3 : Itération :

On applique 16 rondes d'une même fonction. A partir de G_i-1D_i-1 (pour i allant de 1 à 16), on calcule G_iD_i en posant :

G_i=D_i-1.
D_i-1=G_i-1 XOR f(D_i-1,K_i) : XOR est le OU exclusif bit à bit, et f est une fonction de confusion, suite de substitutions et de permutations.
Phase 4 : Permutation finale :

On applique à G₁₆D₁₆ l'inverse de la permutation initiale.
Z=P^-1(G₁₆D₁₆) est le bloc de 64 bits chiffré à partir de x.

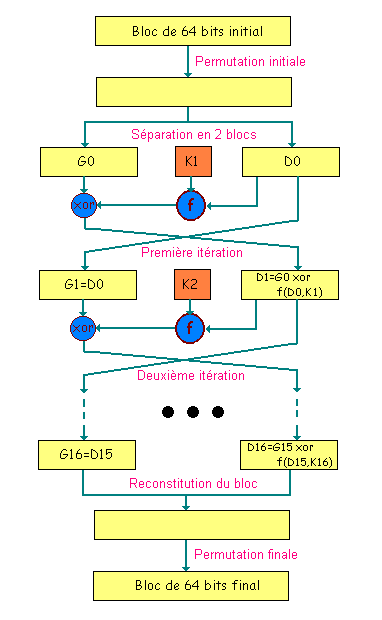
Cet algorithme peut être représenté par le schéma ci après :

Figure 33 : Schéma de l'algorithme DES

L’algorithme DES a régulièrement fait l'objet de polémiques. A l’examen approfondi de celui-ci on constate que toute sa sécurité repose sur la fonction de confusion f, et en particulier à l'intérieur de celle-ci sur des tableaux d'entiers compris entre 0 et 15, aux valeurs mystérieuses. Certains ont affirmé que la NSA, qui a finalisé l'algorithme, a placé dans ces boîtes S des trappes qui lui permettaient de tout décrypter, tout en affirmant que l'algorithme est sûr. Rien n'a toutefois objectivement étayé cette assertion. En particulier, l’algorithme DES a toujours résisté aux travaux des cryptoanalystes non basés sur la force brute.

L’arrêt de mort de l’algorithme DES a été en revanche signé avec l’extraordinaire progression de la puissance des ordinateurs, leur mise en réseau et l’application d’un procédé, connu sous le nom d' « attaque par force brute », utilisé pour retrouver le contenu des communications et qui consiste à essayer toutes les clés possibles^[3]. Leur nombre dépend de la taille de ces clés : pour une clé de n bits, il y a 2ⁿ clés possibles ; la complexité d'un produit est donc bornée par la taille de cet ensemble. Le 17 juin 1997, le DES est cassé en 3 semaines par une fédération de petites machines sur Internet. Et on estime très officiellement (dans un rapport présenté au Sénat Américain) à cette date à quelques secondes le temps nécessaire à un Etat pour percer les secrets d'un message chiffré avec le DES.

7.2.1.A.2.e - L’algorithme Triple – DES :

Face à la faiblesse de l’algorithme DES, la solution a semblé être dans un premier temps l'adoption de l’algorithme surnommé triple DES, algorithme consistant en trois applications de l’algorithme DES à la suite les uns des autres avec 2 clés différentes (d'où une longueur de clé de 2*56 = 112 bits) ou 3 clés différentes (d’où une longueur de clé de 3*56=168 bits). Les deux schémas suivants illustrent les deux implémentations possibles de l’algorithme triple-DES :

Figure 34 : Schéma de l'algorithme Triple – DES – 112 bits

Figure 35 : Schéma de l'algorithme Triple – DES – 168 bits

Si l’algorithme triple DES est largement suffisant à l'heure actuelle en terme de chiffrement d’informations, il est par contre trois fois plus lent que le DES. C'est pourquoi, en janvier 1997, le NIST (National Institute of Standards and Technologies) a lancé un nouvel appel d’offres pour créer un successeur au DES : l’AES (Advanced Encryption System).

7.2.1.A.2.f - L’algorithme AES :

Le cahier des charges de l’algorithme AES comportait les points suivants :

évidemment, une grande sécurité ;
une large portabilité : l'algorithme devant remplacer le DES, il est destiné à servir aussi bien dans les cartes à puces, aux processeurs 8 bits peu puissants, que dans des processeurs spécialisés pour chiffrer des milliers de télécommunications à la volée ;
la rapidité ;
une lecture facile de l'algorithme, puisqu'il est destiné à être rendu public ;
un chiffrement par blocs de 128 bits, les clés comportant 128,192 ou 256 bits.

En réponse à cet appel d’offre, 21 projets ont été déposés. Certains sont l'oeuvre d'entreprises (IBM), d'autres regroupent des universitaires (CNRS), les derniers sont écrits par à peine quelques personnes. Après deux ans d’évaluation, l’algorithme surnommé Rijndael des noms de ses inventeurs Vincent Rijmen et Joan Daemen est finalement choisi.

7.2.1.A.3 - Les principaux inconvénients de chiffrement symétrique :

Le chiffrement symétrique des données, s’il présente l’avantage d’être rapide, présente néanmoins un certain nombre d’inconvénients :

le nombre de clés secrètes à posséder augmente de façon exponentielle en fonction du nombre d’interlocuteurs ;
le changement de clé doit être fréquent de manière à éviter une compromission de clés ;
un mécanisme d’échange de clés de façon sécurisée doit être mis en place.

7.2.1.B - Le chiffrement asymétrique :

La cryptologie asymétrique, encore appelée cryptologie à clé publique s’est attachée à résoudre le problème de la procédure à suivre pour s’accorder initialement sur une clé secrète partagée en chiffrement symétrique. Cette question qui pose peu de problèmes dans le cadre d’applications restreintes à de petits réseaux reliant peu de participants devient fondamentale dans celui de grands réseaux ouverts à l’image d’Internet.

Son principe fondamental est de donner à chaque utilisateur deux clés associées, l’une secrète et l’autre rendue publique.
Afin de chiffrer un message à l’intention d’un utilisateur, l’idée consiste à utiliser la clé publique du destinataire alors que le déchiffrement nécessite la connaissance de la clé privée. Ce concept naturel permet de communiquer de manière confidentielle sans avoir à partager la moindre information secrète initialement.

Les mécanismes permettant la réalisation d’une telle asymétrie se fondent sur l’utilisation d’opérations mathématiques que l’on ne sait pas inverser efficacement d’un point de vue algorithmique.

Exemple : Bob et Alice souhaitent communiquer de façon sécurisée via un chiffrement asymétrique. Les deux interlocuteurs doivent posséder une paire de clés (bi-clé clé publique/clé privée) et le destinataire du message doit posséder la clé publique de l’émetteur.

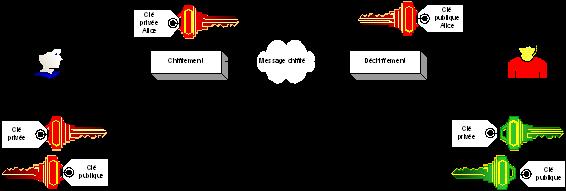
Figure 36 : Chiffrement asymétrique

La cryptologie asymétrique permet notamment :

d’assurer l’authentification de l’émetteur,
d’assurer la confidentialité des données.

Exemple 1 : Authentification de l’expéditeur
Bob veut être certain que l’expéditeur du message est bien Alice. Alice chiffrant le message avec sa clé privée, Bob est certain de l’expéditeur s’il arrive bien à déchiffrer le message avec la clé publique d’Alice.

Figure 37 : Authentification de l’émetteur par chiffrement à clé publique

Exemple 2 : confidentialité des données
Alice veut envoyer des données confidentielles à Bob et veut s’assurer que seul Bob pourra lire les données. Elle chiffre alors les informations à transmettre avec la clé publique de Bob qui sera le seul à pouvoir les déchiffrer à l’aide de sa clé privée.

Figure 38 : Confidentialité des données par chiffrement à clé publique

7.2.1.B.1 - L’algorithme de Diffie-Hellman :

En 1976, Whitfield Diffie et Martin Hellman ont été les premiers à formaliser les concepts de la cryptographie asymétrique et à proposer un algorithme permettant l’échange d’une clé secrète sur un lien non sécurisé.

7.2.1.B.1.a - Principe de fonctionnement de l’algorithme de Diffie-Hellman ;

Illustrons le principe de fonctionnement de l’algorithme de Diffie-Hellman à l’aide d’un exemple d’envoi de message chiffré entre Alice et Bob :

Phase 1 : Alice et Bob partagent deux nombres premiers p et g avec p>g ;

Figure 39 : Algorithme de Diffie-Hellman - Phase 1

Phase 2 : Alice et Bob créent chacun un nombre secret : Y_A et Y_Bbasés sur p, g et sur deux nombres choisis aléatoirement X_a et X_b ;

Phase 3 : Alice et Bob s’échange les deux nombres Y_A et Y_B ;

Figure 40 : Algorithme de Diffie-Hellman - Phase 2

Phase 4 : Alice et Bob calcule la clé de session Z basée sur Y_A et Y_B : cette clé Z servira de clé secrète pour chiffrer et déchiffrer les données dans le cadre de la mise en œuvre d’un algorithme symétrique ;

Figure 41 : Algorithme de Diffie-Hellman - Calcul de la clé secrète

7.2.1.B.2 - L’algorithme RSA :

Le premier cryptosystème asymétrique, RSA, a été proposé en 1978 par Ronald Rivest, Adi Shamir et Leonard Adleman. Il repose sur la difficulté d’un problème proche de celui de la factorisation.
Déchiffrer un message codé avec RSA sans connaître la clé secrète correspondante nécessite d’être capable de résoudre un problème très difficile. Les connaissances actuelles en théorie algorithmique des nombres ne permettant pas de réaliser une telle opération, même en disposant d’une très importante puissance de calcul, une telle hypothèse apparaît bien improbable, d’où une forme de preuve de sécurité ramenant le problème de l’attaque contre une système de chiffrement à un problème mathématique bien défini et étudié. On ne peut cependant pas parler de sécurité inconditionnelle car rien n’exclut que d’importants progrès mathématiques ou matériels ne viennent à bout d’un problème actuellement réputé insoluble. La solidité de l’algorithme RSA tient notamment dans la longueur de la clé publique (on considère qu’a l’heure actuelle un chiffrement à l’aide d’un algorithme RSA basé sur une clé publique de 1024 bits est inviolable. On raconte qu’une armée d'un milliard d'ordinateurs opérant un milliard de calculs à la seconde n'en viendrait à bout avant la fin de l'univers !).

7.2.1.B.2.a - Principe de fonctionnement de l’algorithme RSA :

Reprenons l’exemple d’un échange de message entre Alice et Bob chiffré en utilisant l’algorithme RSA pour mieux comprendre le fonctionnement de cet algorithme.
Si Bob souhaite recevoir des messages chiffrés en utilisant l’algorithme RSA, il procède de la façon suivante :

Phase 1 : Création des clés : Bob crée 4 nombres p, q, e et d :

p et q sont deux grands nombres premiers distincts. Leur génération se fait au hasard, en utilisant un algorithme de test de primalité probabiliste. Le produit de ces deux nombres est noté n ;

e est un entier premier avec le produit (p-1)(q-1) ;

d est tel que ed=1 modulo (p-1)(q-1) c'est-à-dire que ed-1 est un multiple de (p-1)(q-1).

Phase 2 : Distribution des clés : Le couple (n, e) constitue la clé publique de Bob qu’il rend disponible à tous. Le couple (n, d) constitue sa clé privée. Bob garde celle-ci secrète.
Phase 3 : Envoi du message codé : Alice veut envoyer un message chiffré à Bob. Elle le représente sous la forme d'un ou plusieurs entiers M compris entre 0 et n-1. Alice possède la clé publique (n, e) de Bob. Elle calcule C=M^e mod n. C'est ce dernier nombre qu'elle envoie à Bob.
Phase 4 : Réception du message codé : lorsque Bob reçoit C, il calcule à l’aide de sa clé privée D=C^d (mod n). D'après un théorème du mathématicien Euler, D=M^de=M (mod n). Il a donc reconstitué le message initial.

7.2.1.C - Chiffrement symétrique versus chiffrement asymétrique :

Comme les algorithmes à clé publique sont lents à exécuter, on chiffre toujours les messages avec des algorithmes à clé symétrique, et on utilise le dispositif à clé asymétrique pour chiffrer la clé de session générée aléatoirement, comme dans le cas des systèmes à clé secrète.

7.2.1.D - Les fonctions de hachage :

Une fonction de hachage est une fonction qui calcule à partir d’une large chaîne de caractères une chaîne de caractère réduite. Le résultat est dénommé un « digest » ou « empreinte ». Une fonction de hachage permet de représenter les données de façon certaine tout en réduisant la taille utile qui sera réellement chiffrée.
Ce type de fonction ne doit pas être réversible (il doit être impossible de retrouver le message original à partir de l’empreinte ; on parle de fonction à sens unique) et l’algorithme utilisé doit présenter un taux de collision très faible (il doit être extrêmement improbable de trouver deux messages aléatoires M et M’ tels que les résultats du hachage des deux messages soient identiques). Le fonctionnement d’une fonction de hachage peut être résumée par le schéma ci-dessous :

Figure 42 : Fonction de Hachage

Les algorithmes de hachage les plus utilisés sont :

MD4 et MD5 (Message Digest version 4 et 5) qui furent développées par Ron Rivest. MD5 produit des hachés de 128 bits en travaillant les données originales par blocs de 512 bits.
SHA-1 (Secure Hash Algorithm, Algorithme de Hachage Sécurisé version 1), comme MD5, est basé sur MD4. Il fonctionne également à partir de blocs de 512 bits de données et produit par contre des condensés de 160 bits en sortie.
SHA-2 (Secure Hash Algorithm 2) a été publié récemment et est destiné à remplacer SHA-1. Les différences principales résident dans les tailles de hachés possibles : 256, 384 ou 512 bits. Il sera bientôt la nouvelle référence en termes de fonction de hachage.

7.2.1.D.1 - Importance de la taille de l’empreinte :

On peut se demander pourquoi il existe plusieurs tailles de condensés ou encore pourquoi celle-ci est fixe. Il faut garder à l'esprit le but ultime d'un haché qui est d'être le plus court possible, tout en gardant ses propriétés.

Prenons l’exemple d’un haché H, qui présente une longueur de n bits. Nous pouvons d'ores et déjà déduire qu'il n'existe que 2ⁿ hachés de ce type possibles (puisque chaque bit n'a que 2 valeurs possibles, 0 ou 1). Face à l’infinité de textes ou données initiaux (dont la taille, elle, n'est pas fixée), la probabilité de produire un haché qui corresponde à un autre texte original (ou à plusieurs) n’est pas nulle : il s’agit de la mise en évidence du phénomène de collision ou l’on assiste à la perte de la propriété principale d'un condensé, l'unicité.

Le théorème des anniversaires prouve qu'il faut 2^n-1 essais pour trouver une collision au hasard. C'est le chiffre qui sera utilisé pour évaluer la force d'une fonction de hachage. Il ne faut cependant pas négliger le fait que la collision citée précédemment a été obtenue au hasard, ce qui n'est pas exploitable par une personne malveillante dont le but serait de trouver un message significatif et bien formé conduisant au même haché. Ceci augmente considérablement les essais et calculs nécessaires (et le rend quasiment impossible). Quoiqu'il en soit, cela suffit en théorie pour briser la propriété d'unicité de notre condensé...

D'un point de vue pratique, et dans l'état de l'art actuel, il est généralement accepté que 2⁵⁶ calculs représentent un défit réalisable. En conséquence, avec n/2=56 et n=112, le théorème des anniversaires nous indique que les hachés de 112 bits sont faibles et donc insuffisants à l'heure actuelle. De la même manière, les hachés de 128 bits (n/2=64) ne représentent plus une sécurité à moyen terme. C'est pour cela que la norme actuelle est à 160 bits (n/2=80) voire plus dans le cas de SHA-2.

7.2.1.E - Les signatures numériques :

7.2.1.E.1 - La théorie :

La cryptographie asymétrique résout le problème de la mise en accord de clés. Deux problèmes se posent cependant. D’un point de vue pratique tout d’abord, la cryptographie à clé publique nécessite des calculs bien plus complexes que ceux requis par la cryptographie symétrique. Un second problème, bien plus fondamental, est celui de la certification des clés publiques. En effet, il est très facile pour quiconque de générer des couples de clés publiques et secrètes associées. Comment peut-on alors s’assurer que la clé publique que l’on utilise pour chiffrer un message à l’intention d’un correspondant lui appartient effectivement et n’est pas celle d’un pirate ? Une solution consiste à faire signer la clé publique par une autorité certifiant son appartenance à un individu. Ceci nécessite par conséquent de disposer d’un équivalent numérique à la signature manuscrite.
Un algorithme de signature numérique doit concilier diverses propriétés ; le signataire doit pouvoir générer facilement une information attachée à un document numérique quelconque de manière à ce que n’importe qui puisse en vérifier la validité. Toutefois, la vérification ne doit pas donner à celui qui l’exécute la capacité de reproduire une telle signature. La signature électronique jouit d’une propriété fondamentale dite de non-répudiation ; puisque seul le signataire est capable de générer des signatures valides, une telle signature attachée à un document est nécessairement authentique et le signataire ne peut par conséquent pas contester l’avoir générée. La définition d’une signature numérique fait donc apparaître de nouveau une asymétrie entre le processus de signature proprement dit et celui de vérification qui doit être réalisable par n’importe qui. L’idée consiste à utiliser sa clé secrète afin de signer un document de manière à ce que la signature puisse être vérifiée à l’aide de la clé publique uniquement.
La signature permet d’authentifier un message comme provenant bien d’un émetteur. Un problème similaire concerne l’authentification d’une entité ou d’un individu. Dans le monde courant, l’authentification se fait en général par présentation de papiers d’identité dont on suppose qu’ils ne sont ni falsifiables, ni duplicables. Dans un contexte numérique, la modification et la copie sont rendues particulièrement aisées d’où la nécessité de définir de nouveaux mécanismes d’authentification. La notion de preuve interactive à divulgation nulle de connaissance permet de résoudre ce problème de manière particulièrement élégante : afin de démontrer que l’on est bien celui que l’on prétend être, on dispose d’une clé secrète, par exemple deux grands nombres premiers, et d’une clé publique, le produit des deux entiers secrets. On a de plus un certificat signé par une autorité attestant que tel individu possédant telle clé publique est bien celui qu’il prétend être. Afin de faire la preuve de son identité, on produit sa clé publique et le certificat associé et on prouve que l’on connaît bien la clé secrète correspondant à la clé publique, par exemple sa factorisation. Une telle preuve doit convaincre un vérifieur sans pour autant lui fournir d’information sur le secret afin d’éviter qu’un espion ou bien que le vérifieur lui-même puisse ensuite se faire passer pour vous. C’est ainsi que l’on a défini la norme de signature DSS (Digital Signature Standard).

7.2.1.E.2 - Le mécanisme de la signature numérique :

D’un point de vue technique, la signature numérique est une empreinte chiffrée jointe au document originel. Elle peut ainsi être utilisée pour prouver l’identité de l’expéditeur et l’intégrité du document. De manière à détailler le mécanisme de la signature numérique, reprenons l’exemple d’un message envoyé par Alice à Bob, message pour lequel Alice veut assurer être l’expéditeur :

Phase 1 : Création de la signature numérique :

Alice et Bob décident de l’algorithme de chiffrement à clé publique à utiliser : ils créent leurs bi-clés (clé publique/clé privée) et s’échangent leur clé publique ;

Ils décident de l’algorithme de la fonction de hachage à utiliser pour vérifier leur signature ;

Alice crée une empreinte de son message à envoyer à l’aide de la fonction de hachage et chiffre celle-ci avec sa clé privée. Cette empreinte chiffrée est une signature numérique jointe au document original ;

La combinaison du document et de la signature numérique est envoyée à Bob.

Figure 43 : Création d’une signature numérique

Phase 2 : Vérification de la signature numérique :

Bob déchiffre l’empreinte chiffrée à l’aide de la clé publique d’Alice. Il conserve cette empreinte ;

Bob crée une empreinte du message à l’aide de la fonction de hachage ;

Bob compare l’empreinte obtenue avec l’empreinte originale : s’ils sont identiques, l’intégrité du message et l’authentification de l’émetteur sont assurés.

Figure 44 : Vérification d’une signature numérique

7.2.1.E.3 - Les certificats numériques :

Si les notions de signatures et de certificats numériques sont souvent liées c’est qu’il s’agit de deux mécanismes opposés. S’il est vrai que la signature numérique permet d’authentifier de façon formelle l’expéditeur, le certificat numérique permet lui de s’assurer de l’identité d’un destinataire potentiel.

Un certificat numérique est un message signé numériquement à l’aide de la clé privée d’un tiers de confiance reconnu par les deux parties (on parle de Certificate Authority). Le standard « de jure » reconnu par tous est le format X509 version 3 (cf. chapitre sur les acteurs du marché) et contient au minimum les informations suivantes :

le numéro de version X509 ;
le numéro de série associée au certificat ;
l’algorithme de signature utilisé ;
l’émetteur du certificat ;
les dates de début et de fin de validité du certificat ;
la clé publique de l’objet du certificat ;
la signature de l’autorité émettrice.

7.2.1.E.3.a - La vérification du destinataire à l’aide des certificats numériques :

De manière à détailler le mécanisme, reprenons l’exemple d’un message envoyé par Alice à Bob, message pour lequel Alice veut s’assurer que Bob est bien le destinataire qu’il prétend être :

Phase préalable : Création du certificat de Bob

Bob a transmis à une autorité de certification un certain nombre d’informations constituant une véritable « fiche d’identité » ;

L’autorité de certification a :

Vérifié les informations fournies par Bob ;
Ajouté ses propres informations (clé publique) aux informations fournies ;
Calculé une empreinte du tout chiffrée avec la clé privée de l’autorité de certification ;
Signé un certificat au nom de Bob à l’aide de cette empreinte.

Phase 1 : Vérification de l’identité du destinataire :

Alice récupère auprès de l’autorité de certification le certificat de Bob ;

Alice calcule l’empreinte correspondante aux informations contenues dans le certificat ;

Alice déchiffre la signature du certificat à l’aide de la clé publique de l’autorité ;

Si les deux empreintes sont identiques, Alice a bien affaire a Bob.

Ce mécanisme peut être résumé par le schéma suivant :

Figure 45 : Vérification du destinataire à l’aide d’un certificat numérique

7.2.1.E.3.b - La mise en application des certificats numériques : l’infrastructure de gestion de clés

Le mécanisme de certificats numériques est mis en œuvre au sein d’architectures logicielles et matérielles complexes nommées IGC (infrastructure de gestion de clés) ou PKI (Public Key Infrastructure) ou encore ICP (Infrastructure à Clés Publiques).
Sans vouloir présenter de façon exhaustive et complexe, l’ensemble des mécanismes mis en œuvre au sein d’une IGC, ce paragraphe se borne à en présenter les grandes lignes et les principaux acteurs.

- Le fonctionnement simplifié d’une IGC :

Les mécanismes d’une IGC s’appuient fondamentalement sur les mécanismes associés aux certificats numériques. La complexité majeure dans la mise en œuvre d’une IGC repose sur l’ensemble des procédures organisationnelles à mettre en œuvre permettant de garantir :

L’assurance de la véracité des informations communiquées par l’utilisateur lors de la demande de certificat ;
Le caractère réellement aléatoire des nombres utilisés dans les différents algorithmes permettant la génération du certificat ;
L’assurance de la délivrance du certificat au bon propriétaire ;
la validité d’un certificat à un instant donné.

Une autorité de certification peut être elle même certifiée par une autorité de certification de niveau supérieur. Dans le cas d’un utilisateur devant pouvoir reconnaître la validité de certificats délivrés par une autorité de certification donnée, les choix suivants sont possibles :

l’utilisateur admet l’autorité de certification comme autorité de confiance ;
l’utilisateur admet une autorité de niveau supérieur comme autorité de confiance.

- Les principaux acteurs d’une IGC :
- L’autorité locale d’enregistrement :

Cette autorité locale d’enregistrement est en charge de recueillir les informations communiquées par l’utilisateur lors de la demande initiale ou du renouvellement d’un certificat. Cette autorité est également en charge de la délivrance des nouveaux certificats. Elle génère des demandes de certificats à l’attention de l’autorité d’enregistrement.

- L’autorité d’enregistrement :

Cette autorité d’enregistrement concentre les demandes de certificats émanant des autorités locales d’enregistrement et prépare les certificats à valider.

- L’autorité de certification :

Cette autorité est la plus importante de toutes puisque son rôle est de signer les certificats à l’aide de sa clé privée. L’importance de l’alea utilisé dans la génération de la paire clé privée/clé publique y est fondamentale.

- L’autorité de séquestre :

Le but de cette autorité est de pouvoir conserver ou régénérer un certificat de chiffrement délivré à un utilisateur de manière à être toujours capable de déchiffrer un message de celui-ci dans les cas suivants :

le certificat de chiffrement utilisé n’est plus valable ;
le certificat de chiffrement utilisé est perdu ou détruit.

Il est important de noter qu’il est strictement interdit de séquestrer les certificats destinés à la signature des messages par les utilisateurs.

- La publication des listes de révocation de certificats :

Une liste de révocation de certificats (on parle de CRL, Certificats Revocation List) contient la liste des certificats invalidés ou révoqués par une autorité de certification. L’emplacement permettant la consultation de cette liste est systématiquement intégré au sein de chaque certificat délivré par une autorité de certification.
Il est important de noter qu’il appartient aux logiciels clients de consulter ou non cette liste avant d’affirmer la validité d’un certificat donné.

- L’annuaire LDAP :

Il est courant de stocker l’ensemble des certificats générés par une autorité de certification au sein d’un annuaire au format LDAP. Les certificats font alors partie intégrante de la définition des utilisateurs stockée au sein de l’annuaire.

- Schéma de fonctionnement d’une IGC :

Le fonctionnement d’une infrastructure de gestion de clés peut être résumé par le schéma suivant :

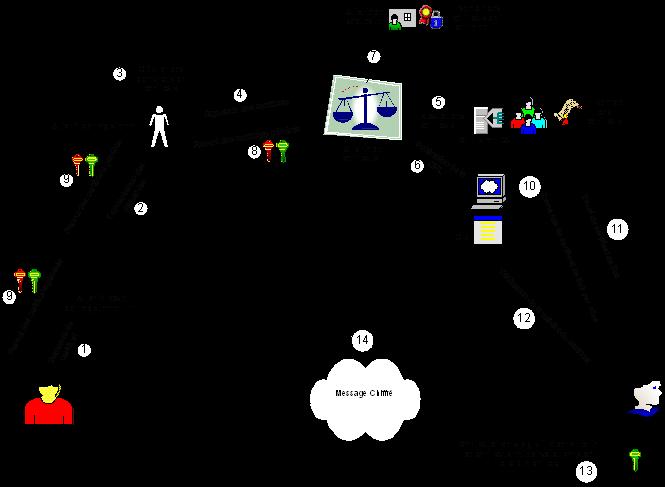Figure 46 : Le fonctionnement simplifié d’une infrastructure de gestion de clés

^[2] Ces normes ne sont pas toujours publiées ; cependant, dans la mesure où elles ont vocation à être fournies aux différents constructeurs dans tous les pays, leur caractère confidentiel peut être considéré comme relatif.
^[3] La complexité de cette attaque par force brute dépend de la vitesse d'exécution de l'algorithme et de la puissance de calcul utilisée ; à titre indicatif, pour certains algorithmes courants type DES, il est possible de retrouver une clé de 40 bits en quelques heures ou dizaines d'heures de PC. Cette complexité est multipliée par un facteur 65 000 si l'on passe à 56 bits ; pour 128 bits, effectuer ce type de recherche exigerait des ressources très largement non disponibles à l'heure actuelle.